El quinto en discordia es aquél personaje de teatro que, sin ser el héroe o la heroína, el confidente o el villano, ejerce una importante influencia para el desarrollo de la trama. En la geometría el quinto postulado desempeña este papel.
En esta entrada vamos a hablar sobre GEOMETRIA(s) NO EUCLÍDEA(s). Es decir, las que no satisfacen todos los postulados de Euclides, en especial las que no satisfacen el quinto postulado.

La palabra geometría es la combinación de dos palabras del griego antiguo, GEO que significa tierra y METRÍA que significa medida. Esta rama de las matemáticas se ocupa de la forma, tamaño, y posición relativa de figuras planas o del espacio y de sus propiedades.

Fueron los griegos, y en especial Euclides, los que la desarrollaron la geometría de una forma axiomática y constructiva. Para evitar que la intuición o la percepción nos lleven a engaño Euclides propone partir de unas afirmaciones básicas y sencillas, los axiomas o postulados.

Postulado I – Si tenemos dos puntos podemos trazar una recta que pase por estos dos puntos. (Euclides presupone que esta recta es única).

Postulado II – Si tenemos un segmento podemos prolongarlo indefinidamente.

Postulado III – Si tenemos un punto O y un segmento podemos trazar una circunferencia con centro en O y radio ese segmento.

Postulado IV – Todos los ángulos rectos son iguales.

Postulado V – Dada una recta r y un punto P exterior a ella, existe una única recta que pasa por el punto P y es paralela a la recta r. Los matemáticos se pasaron siglos tratando de probar que esto era un Teorema que se deducía de los cuatro primeros postulados. Pero fracasaron.

No fue hasta principios del siglo XIX cuando varios matemáticos como Gauss, Bolyai, Lobachevski y Riemann, se percataron de que no solo no era posible demostrar el quinto postulado a partir de los cuatro primeros, sino que podíamos considerar otros quintos postulados diferentes.

Por ejemplo, podemos imponer que por un punto exterior a una recta no pase ninguna paralela (GEOMETRÍA ELÍPTICA) o que por un punto exterior a una recta pasen rectas paralelas pero no necesariamente solo una (GEOMETRÍA HIPERBÓLICA).

Un ejemplo de lo primero lo constituye la geometría esférica. Imaginemos una la superficie de una esfera. Las rectas que unen los puntos de dicha esfera serán las trayectorias de menor distancia entre dichos puntos. Estas trayectorias son llamadas CÍRCULOS MÁXIMOS.
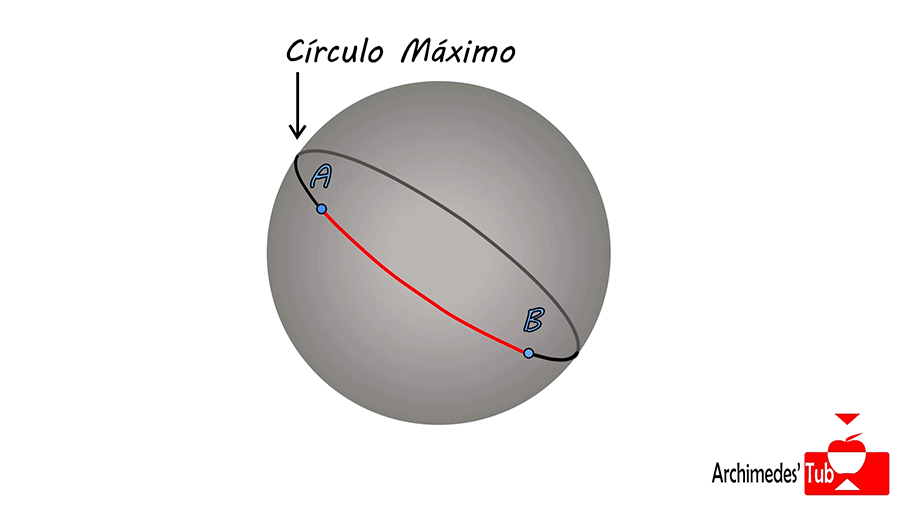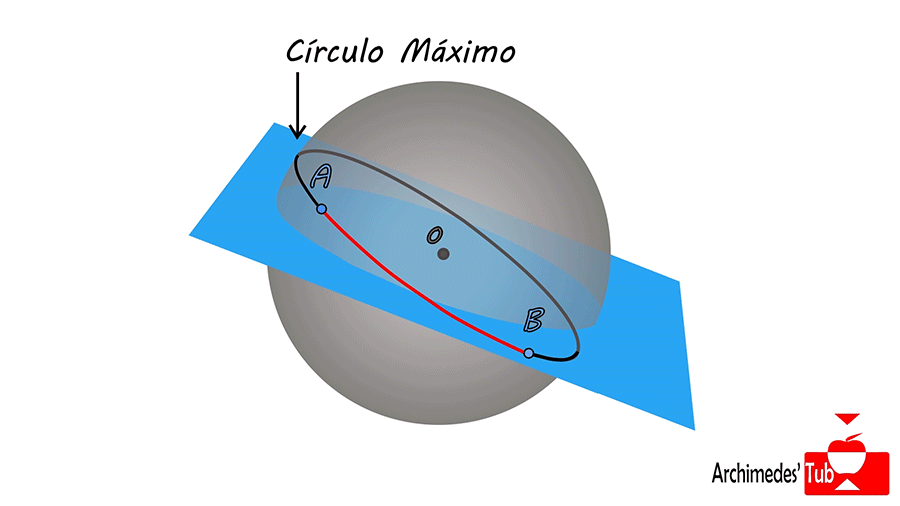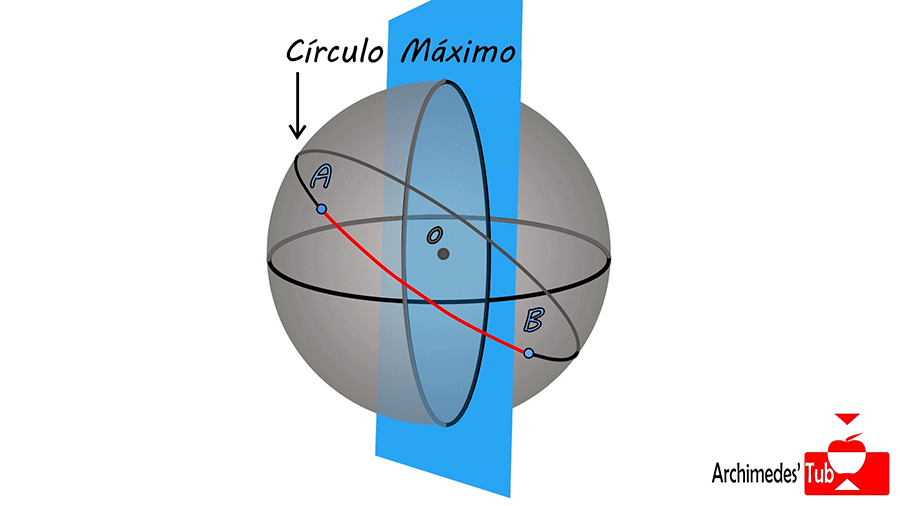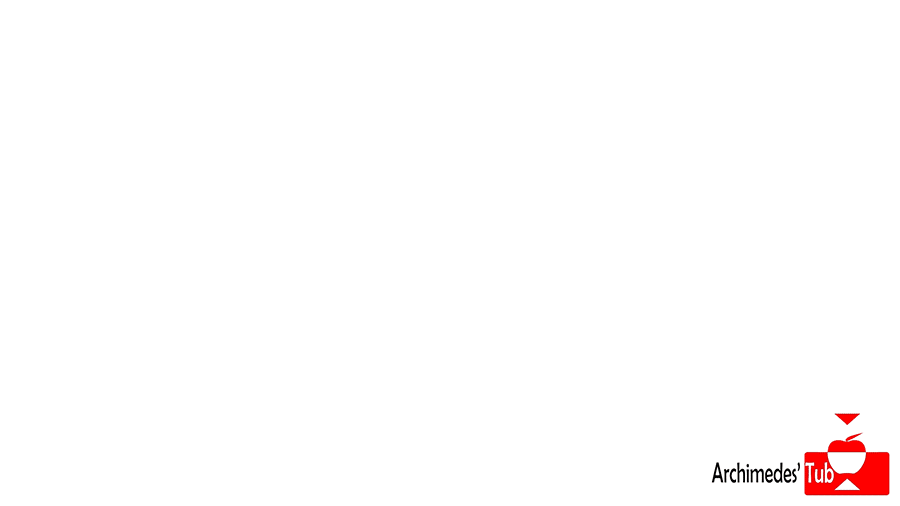
Estos círculos máximos se obtienen considerando el plano que pasa por los dos puntos y el centro de la esfera (tres puntos determinan un plano) y tomando la intersección del plano con la esfera. Ejemplos de círculos máximos son el ECUADOR, o los MERIDIANOS.

¡Pues la geometría esférica no satisface el quinto postulado de Euclides! Por ejemplo, si consideramos un punto externo al ecuador, cualquier plano que pase por este punto y el centro de la esfera interseca al ecuador.

Durante un tiempo se pensó que la geometría hiperbólica no dejaba de ser una abstracción propia del mundo matemático que como tal solo podía interesar a estos. Y que incluso pudiera ser inconsistente llegándose a una contradicción en algún momento partiendo de los axiomas.
Sin embargo, en 1868 Eugenio Beltrami presentó un modelo diferencial de geometría hiperbólica. En concreto, propuso que esta geometría podría realizarse en una superficie de curvatura negativa constante, ¡LA PSEUDOESFERA!
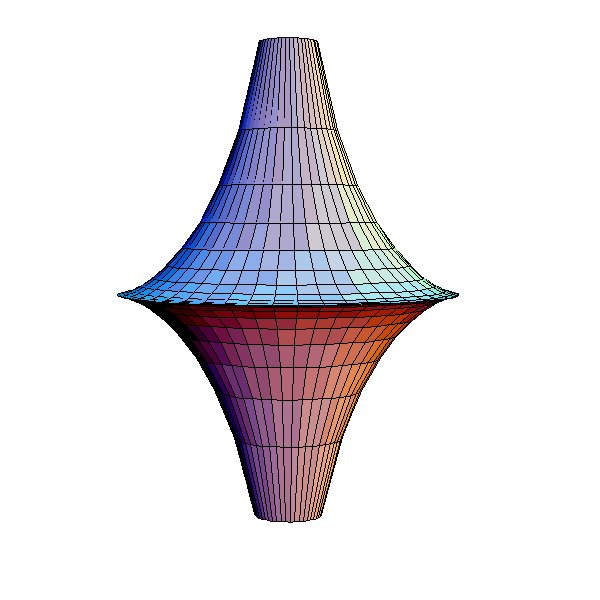
Esto probaba que, si la geometría hiperbólica era inconsistente, entonces ¡También lo era la geometría euclídea de toda la vida! Veamos este METATEOREMA con más detalle a través del modelo más sencillo que propuso posteriormente Felix Klein.

Dentro del plano consideramos como un disco sin su borde. Los puntos del modelo son los puntos del disco abierto y las rectas son cuerdas en el disco (sin los extremos). Dos puntos cualesquiera están unidos por una única cuerda, aunque la distancia d(P,Q) no es la usual.

También podemos definir el ángulo entre dos rectas de una forma no usual, pero ahora viene lo importante. Utilizando los Postulados del plano podemos DEMOSTRAR los cuatro primeros postulados para este modelo, aunque claramente se satisface ¡el quinto postulado HIPERBÓLICO!

De este modo tenemos un modelo hiperbólico DENTRO del plano Euclídeo. Si llegáramos a una contradicción a partir de los axiomas de la geometría Hiperbólica, ésta necesariamente vendría de los axiomas Euclídeos. Ambas Geometrías están condenadas a ser consistentes o no de la mano.
Y si hay algún aficionado al ajedrez que haya llegado hasta aquí, disfrutará mucho con este vídeo. (Os podéis suscribir a nuestro canal 😃)
