En matemáticas hay resultados valiosos fruto de sencillas y elegantes demostraciones. Uno de nuestro preferidos es la fórmula de Euler para poliedros convexos. Nos hemos propuesto demostrar este teorema usando pocas palabras y unos cuantas imágenes.
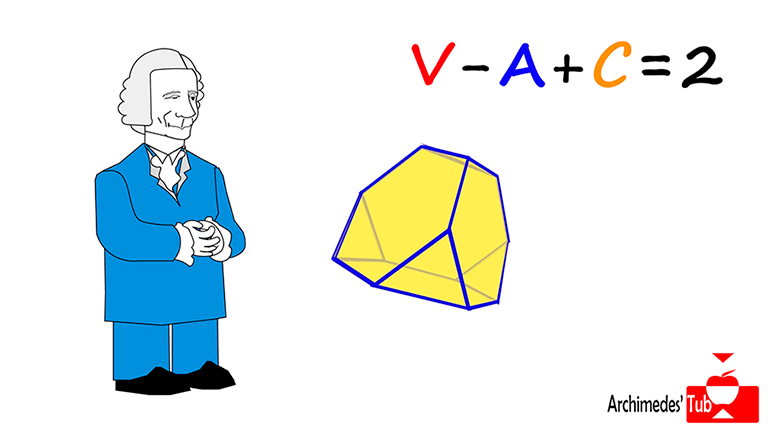
Si consideramos un poliedro, una figura formada por polígonos que encierran una región del espacio. Y además le exigimos que sea convexo, que no tenga recovecos ni agujeros, y contamos sus vértices (V), le restamos sus aristas (A) y le sumamos sus caras (C), ¡SIEMPRE SALE 2!
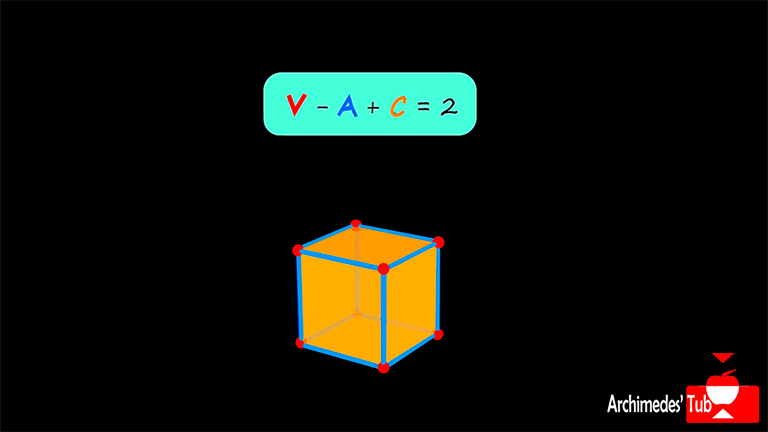
Pese al nombre que lleva la fórmula, no fue Euler el primero en demostrarla. Su historia se extiende a lo largo de 200 años y en ella intervienen gigantes como Descartes, Legendre, Cauchy (y Euler). Seguimos la de Augustin-Louis Cauchy (1789-1857) y la visualizamos con el cubo:
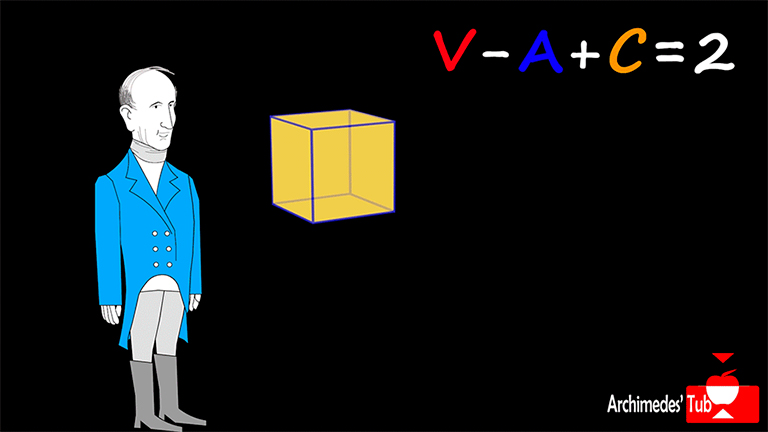
En primer lugar, eliminamos una cara del poliedro. Situamos una bombilla encima del hueco y proyectamos su imagen sobre un plano, obtenemos una figura plana con el mismo número de vértices, aristas y caras que el poliedro sin la cara eliminada.
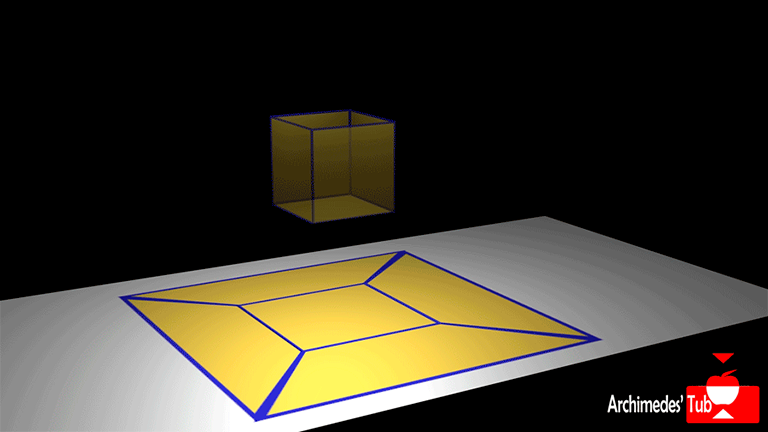
Razonamos sobre esta figura plana haciendo cambios que no afectan al total V-A+C. Trazamos una diagonal sobre toda cara que no sea un triángulo. Cada arista que añadimos (que resta) divide una cara en dos, apareciendo una nueva cara (que suma). ¡V-A+C no ha cambiado!
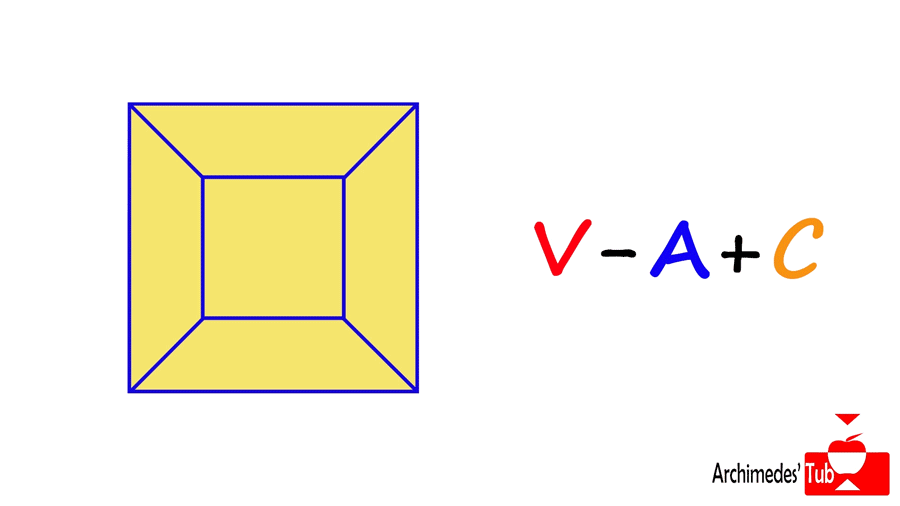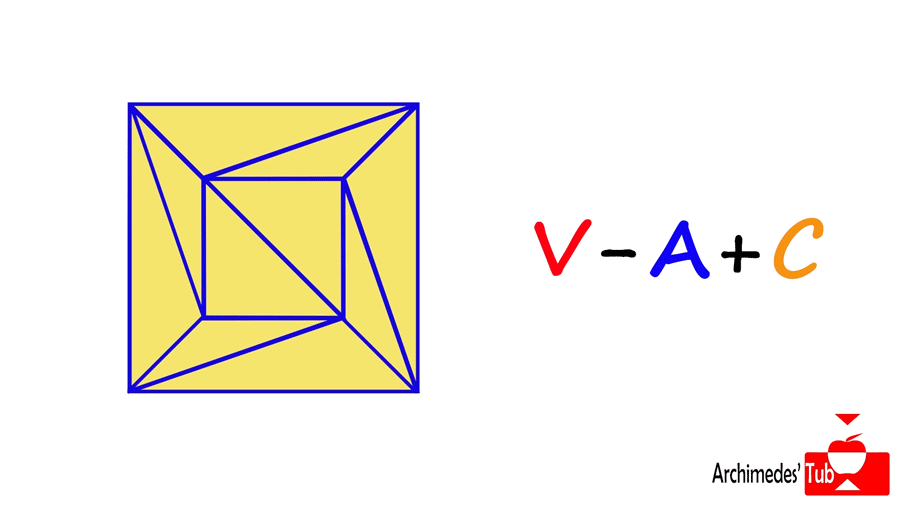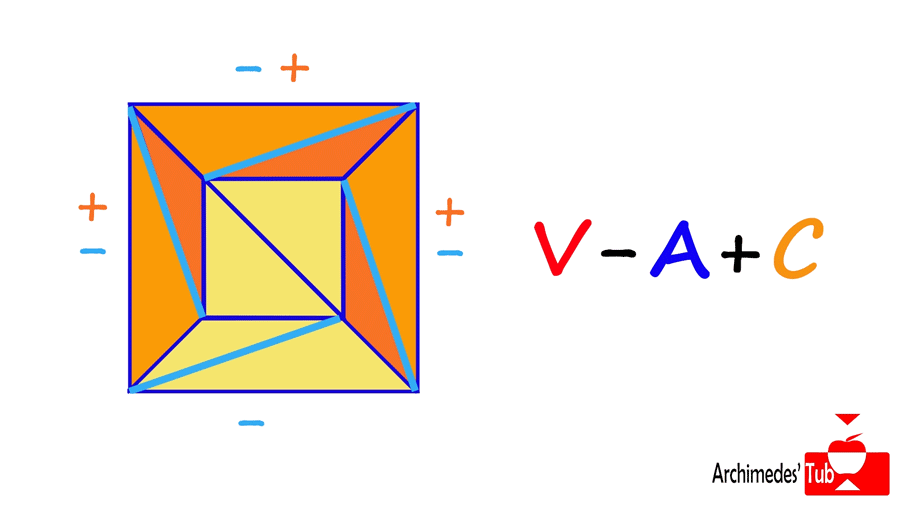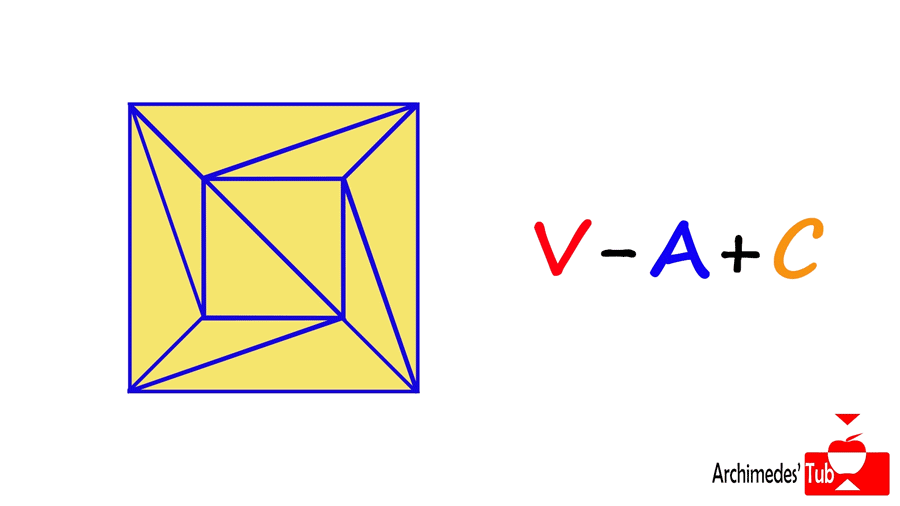
A continuación, eliminamos todo triángulo que tenga exactamente una arista externa. De este modo eliminamos una arista (que resta) y una cara (que suma) por cada triángulo eliminado, y de nuevo el número V-A+C no cambia.
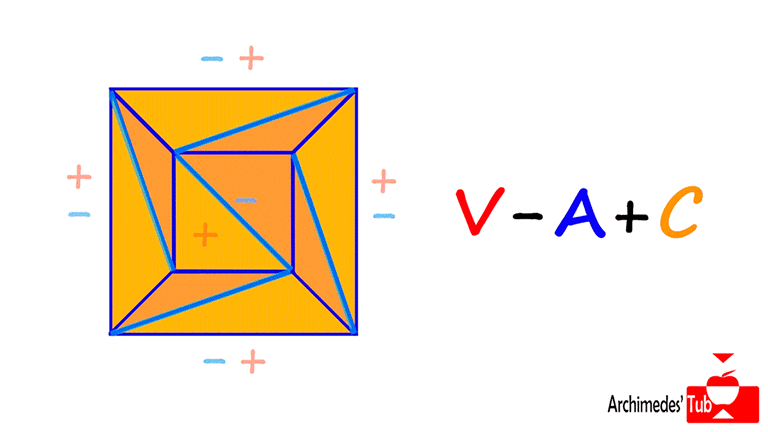
Finalmente eliminamos los triángulos con DOS aristas externas. En este caso se eliminan dos aristas (que restan) pero también un vértice (que suma) y una cara (que suma) por cada triángulo. Nuevamente el número V-A+C no varía.
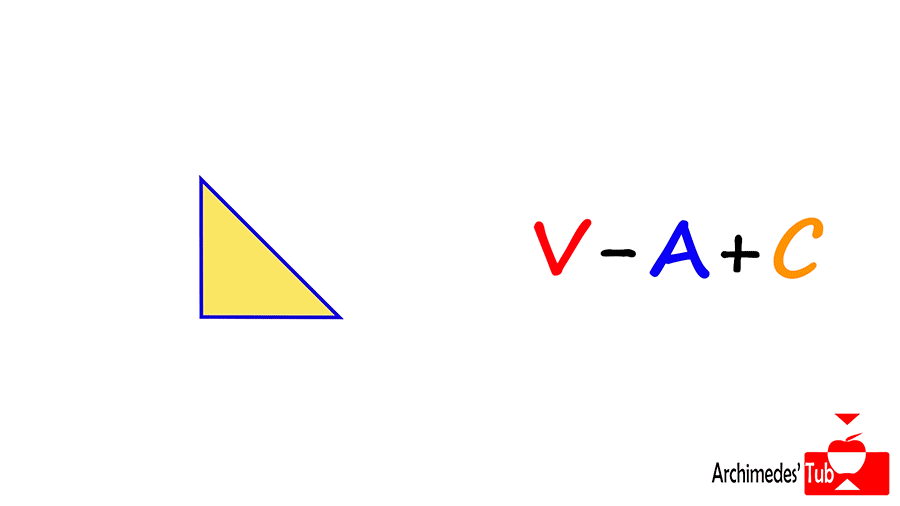
Repitiendo este proceso llegaremos a un único triángulo. Si echamos la cuenta tendremos 3 vértices, 3 aristas y 1 cara. 3-3+1=1. Y recordemos que al principio de la demostración le habíamos quitado una cara al poliedro, así que tenemos V-A+C=2. ¡Como afirmaba Euler!
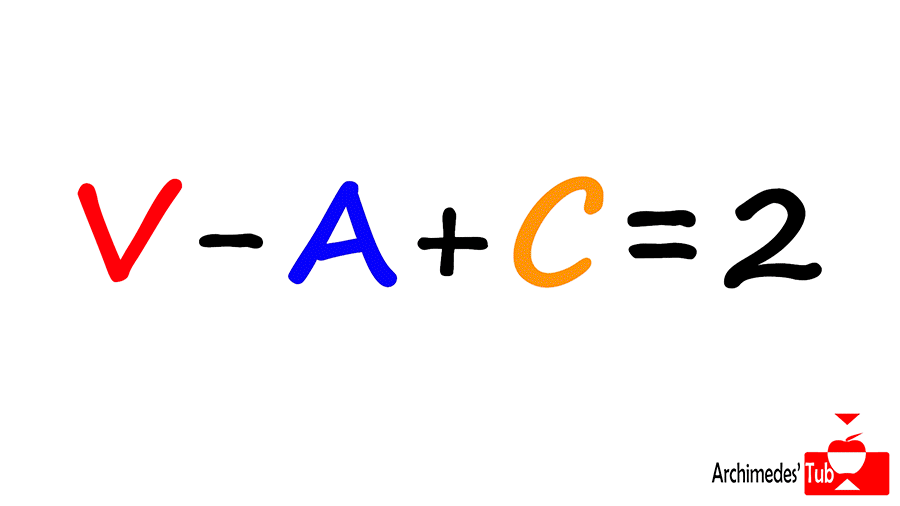
En nuestro canal de youtube podéis encontrar un vídeo con esta demostración ampliada:
Si este vídeo te ha gustado SUSCRÍBETE, haz click en «Me gusta» y COMPÁRTELO.
📚 Bibliografia Recomendada
1️⃣ Para los más jóvenes, una forma de introducirse en la fórmula de Euler y los poliedros es sin duda ‘El diablo de los números’ de Hans Magnus Enzensberger. En la décima noche Robert aprenderá la fórmula de Euler para grafos y poliedros y conocerá los sólidos platónicos.
2️⃣Los interesados en una referencia más avanzada pueden consultar “Mathematics and Plausible Reasoning. Volume I” de George Polya.
En el Capítulo III “Induction in solid geometry” se puede encontrar un análisis exhaustivo de la fórmula de Euler desde el punto de vista de la heurística. Además en el anexo con material adicional puede encontrarase en los ejercicios el trabajo de Descartes sobre poliedros (ver páginas 56, 57 y 58).
3️⃣ Para una lectura emocionante sobre Euler, los orígenes de la topología y la fórmula de Euler, sin duda la referencia obligada es “Euler’s Gem” de David S. Richeson
Uno de los atractivos de este libro es en particular el capítulo dedicado a la historia del teorema de clasificación de superficies. Imprescindible lectura.

Leonhard Euler, ha sido para mi uno de los más grandes matemáticos de todos los tiempos, y su característica inalienable en su desempeño fue la elegante capacidad de síntesis, bellamente presentada en sus ecuaciones!!!
Atte. Alfredo Durand El Cuervo
Muchísimas gracias por tu comentario. No podemos estar más de acuerdo.
Un saludo.