No vamos a hablaros de ninguna banda musical indie, sino de August Ferdinand Möbius matemático y astrónomo alemán que murió un día como hoy hace exactamente 150 años.
Aunque también ha sido bautizado con su nombre un cráter lunar y un asteroide, hablaremos hoy aquí de uno de sus objetos matemáticos, LA BANDA O CINTA DE MÖBIUS.
A pesar de su simplicidad, el objeto que vamos a describir tiene una importancia fundamental en TOPOLOGÍA.
Esta disciplina estudia los espacios como si se trataran de objetos de goma. Podemos estirarlos, retorcerlos, doblarlos, pero nunca rasgarlos o romperlos.
Lo importante en Topología es la CONTINUIDAD.
Decimos que la topología es una especie de geometría en la que no medimos cosas (ángulos, áreas, longitudes,…), solo nos interesa la FORMA.
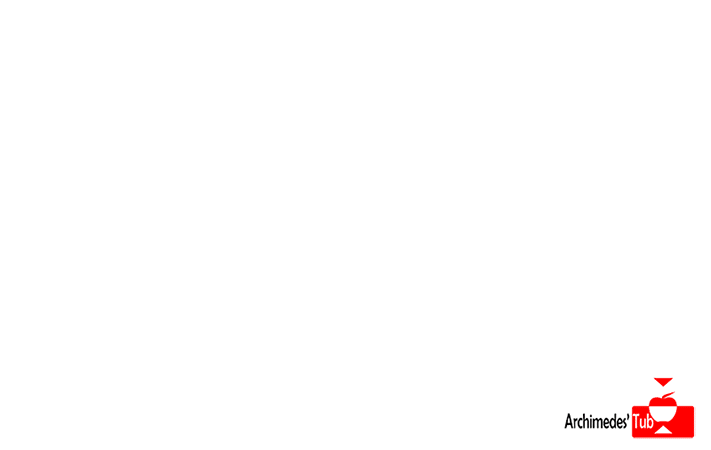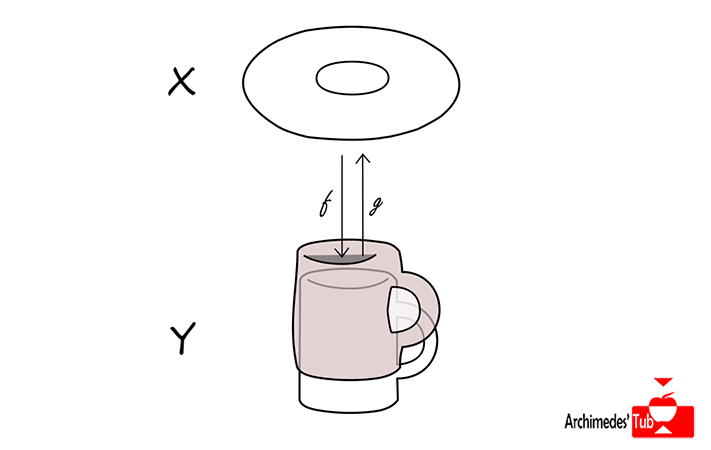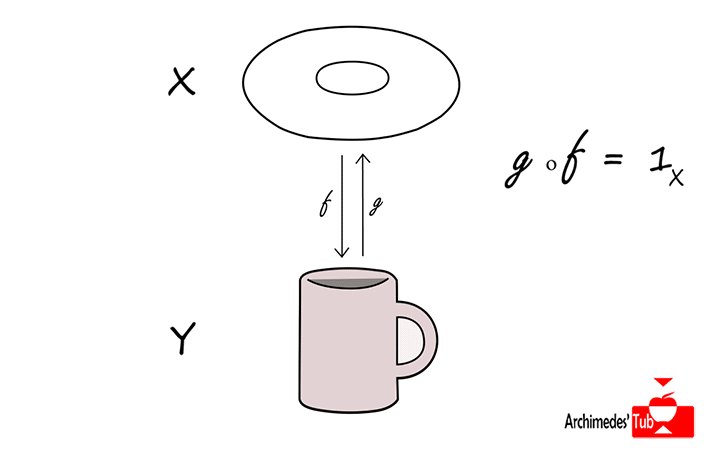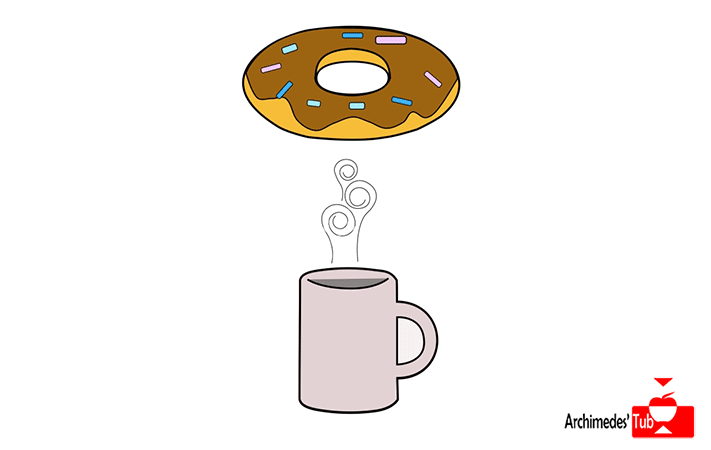
Un ejemplo de espacio (topológico) sin rebuscar demasiado es una recta continua. Aunque también podemos quedarnos con una parte de la recta como por ejemplo el intervalo [0,1] formado por todos los números entre 0 y 1.
Una vez que tenemos algunos ejemplos de espacios topológicos nos gustaría tener algún método o mecanismo para crear nuevos espacios a partir de estos. Unos de estos métodos es el producto cartesiano (en honor de René Descartes).
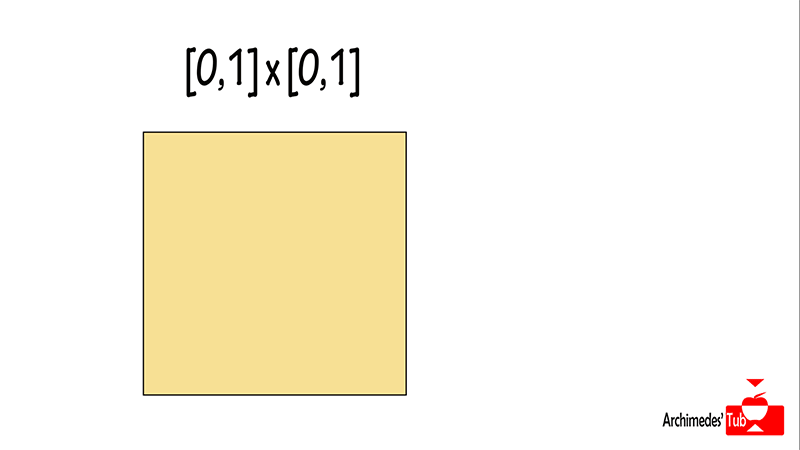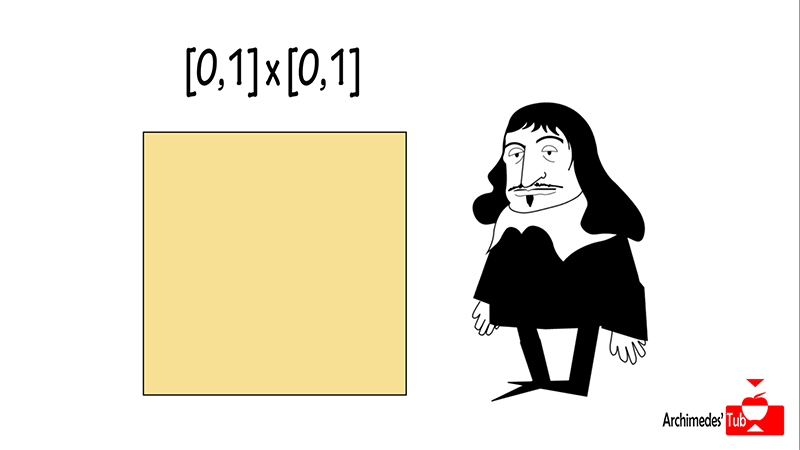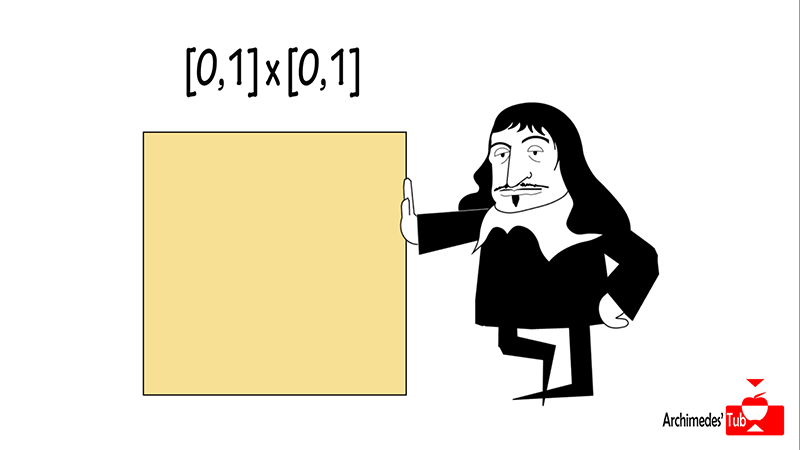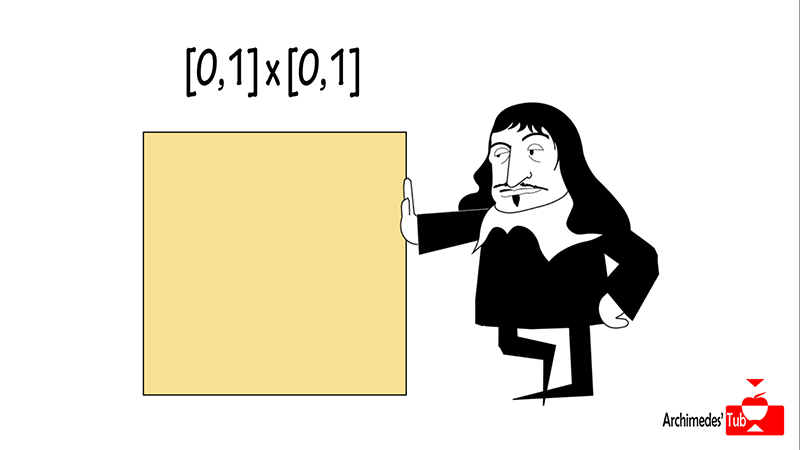
Por ejemplo, si partimos del intervalo [0,1], el producto cartesiano del intervalo consigo mismo [0,1]x[0,1] está formado por pares de números (x, y) donde x e y están en [0,1], esto es, son números entre 0 y 1. El producto [0,1]x[0,1] no es más que un cuadrado de lado 1.
Otro ejemplo más complicado de visualizar sería el producto de una circunferencia C consigo misma. El producto CxC estaría formado por pares (a, b) donde tanto a como b son puntos de la circunferencia y el resultado es un espacio con forma de flotador llamado TORO.
Pero no nos distraigamos de nuestro cometido. Otra forma más sofisticada de obtener nuevos espacios topológicos a partir de otros conocidos consiste en identificar, esto es, pegar puntos de un espacio entre sí.
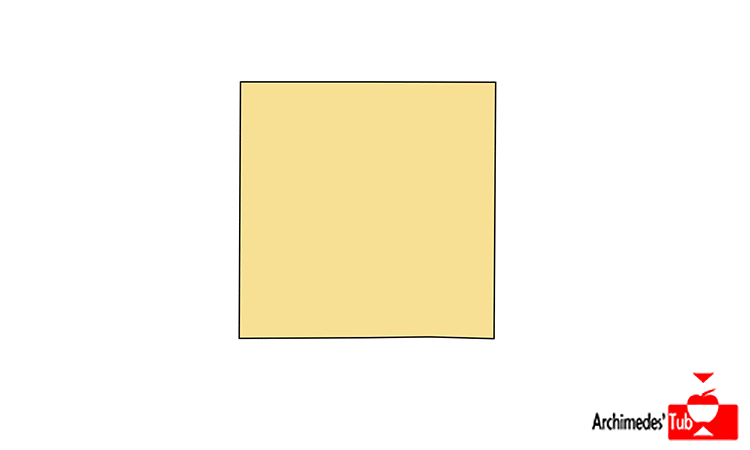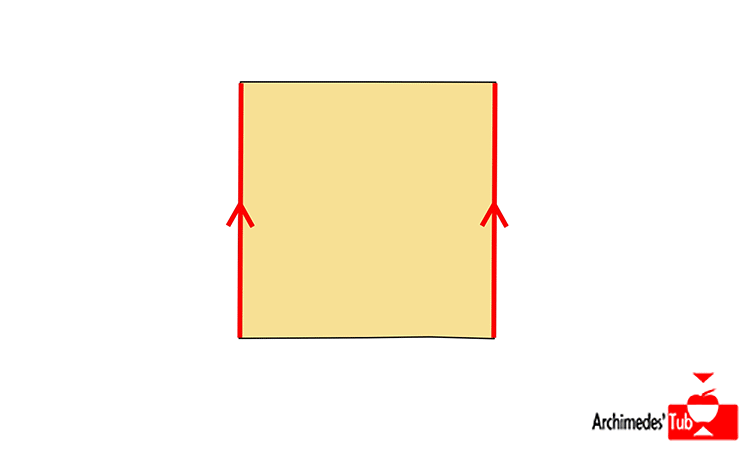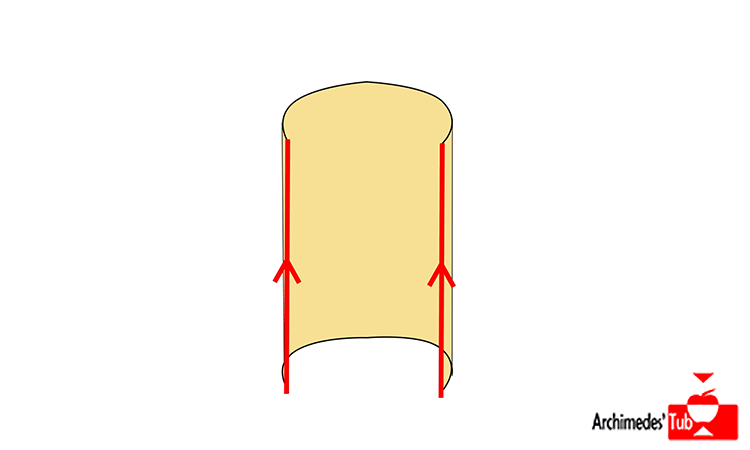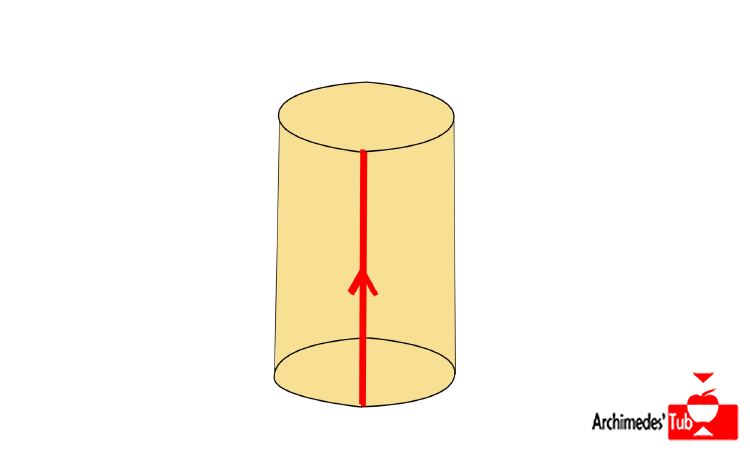
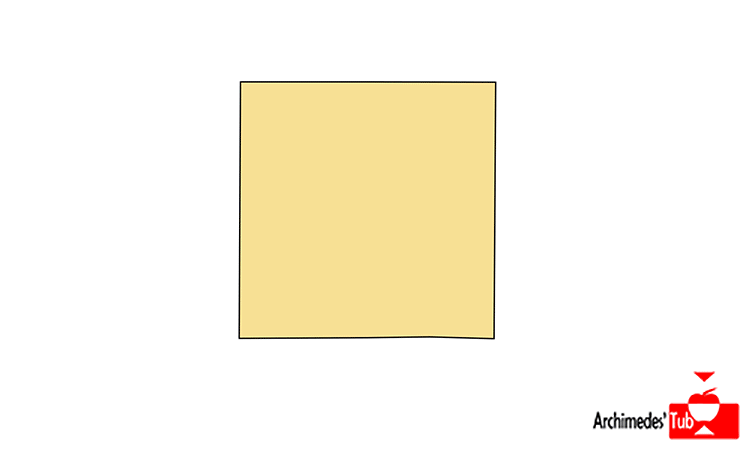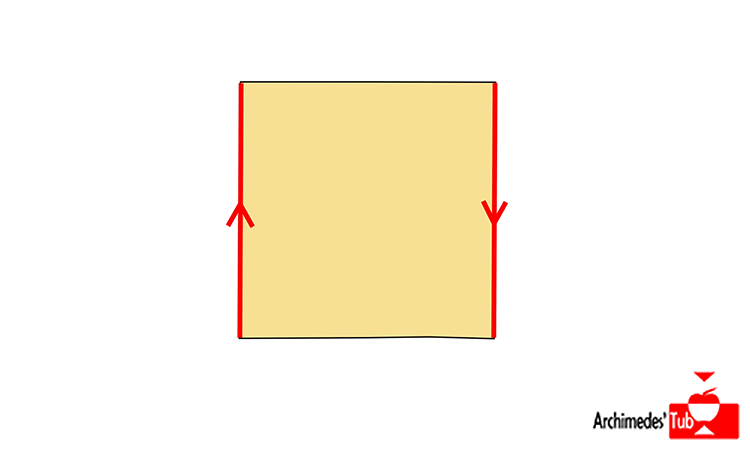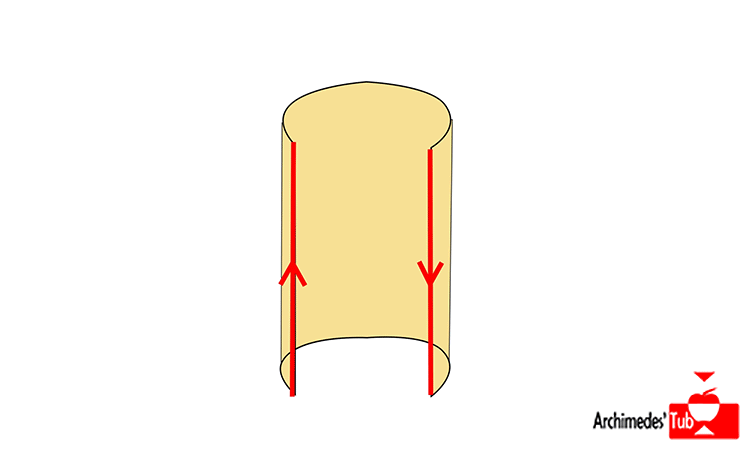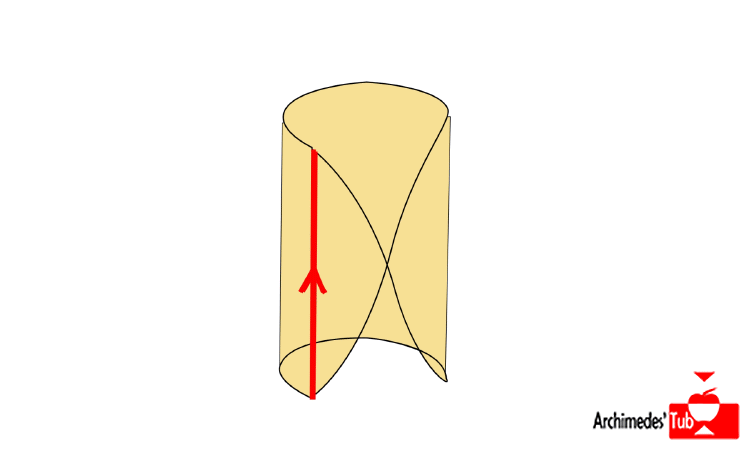
Si partimos del cuadrado [0,1]x[0,1] e identificamos los puntos de los bordes verticales del cuadrado entre sí, es decir (0,x) lo identificamos con (1,x), cosa que indicamos en el dibujo con las dos flechas apuntando en el mismo sentido, lo que obtendríamos en ¡UN CILINDRO!
Pues ya hemos llegado a donde queríamos. Hagamos lo siguiente: en vez de identificar los puntos de los bordes verticales que están a la misma altura como antes, identifiquemos el punto (0,x) con el (1,1-x), es decir, una flecha apunta hacia arriba y la otra hacia abajo.
Lo que obtenemos es uno de los objetos matemáticos más sencillos y sorprendentes con los que nos podemos topar. ¡LA CINTA DE MÖBIUS!
Aunque para ser justos la cinta fue descubierta simultáneamente por Möbius y Johan Benedict Listing.
(Como simple anécdota, deciros que Listing fue precisamente el matemático que introdujo el término “Topología”)
Si la inspeccionamos con un poco de cuidado nos damos cuenta que a pesar de tener apariencia de cinta (como el cilindro), si una hormiga empezara a andar por el borde de esta figura lo recorrería completamente sin tener que atravesarla.
Si en vez de andar la hormiga por el borde se diera un paseo por su superficie veríamos que la cinta de Möbius no es que solo tenga un borde, es que ¡SOLO TIENE UNA CARA!
Pero la cosa puede ponerse mucho más seria…
Supongamos que la hormiga tiene un reloj. Se da un paseo y aparece de nuevo en el punto de partida (mentiríamos si dijéramos “por la otra cara”, pues solo hay una). ¡El reloj movería sus manecillas en sentido contrario!
Este fenómeno que le ocurre a la cinta de Möbius se resume en que la superficie es NO-ORIENTABLE. Es decir, no podemos hablar de derecha o izquierda, de sentido de las agujas del reloj, pues podría ocurrir que tras un paseo el mundo estuviera del revés.
Este objeto matemático no es una mera curiosidad pues su descubrimiento fue solo un paso más en un largo camino hacia la formalización del concepto de superficie.
Y tanto Möbius como Listing, junto a otros matemáticos entre los que están Bernard Riemann, Félix Klein o Camille Jordan, pusieron las bases para la demostración de uno de los mayores logros matemáticos de la humanidad: El Teorema de clasificación de superficies.
Este Teorema afirma que toda superficie compacta conexa es o bien:
1) Una esfera o una suma conexa de toros si es orientable
2) Un plano proyectivo o una suma conexa de planos proyectivos si no es orientable
Hay algunos conceptos que no he introducido en este enunciado: La suma conexa es otro método para obtener espacios a partir de otros dados. Consiste en “recortar” un par de discos de dos espacios y pegarlos por el borde del disco recortado.
Y el segundo concepto no definido en este enunciado es el de plano proyectivo que es un espacio que se obtiene a partir de un cuadrado (al igual que nuestra cinta de Möbius) pero identificando tanto los bordes verticales como los horizontales de forma inversa.
En palabras del gran matemático del siglo XX, V. Arnold, la demostración del Teorema de Clasificación de Superficies es un hito de la humanidad comparable al descubrimiento de América o de los Rayos X, y como tal debería estudiarse en las escuelas.
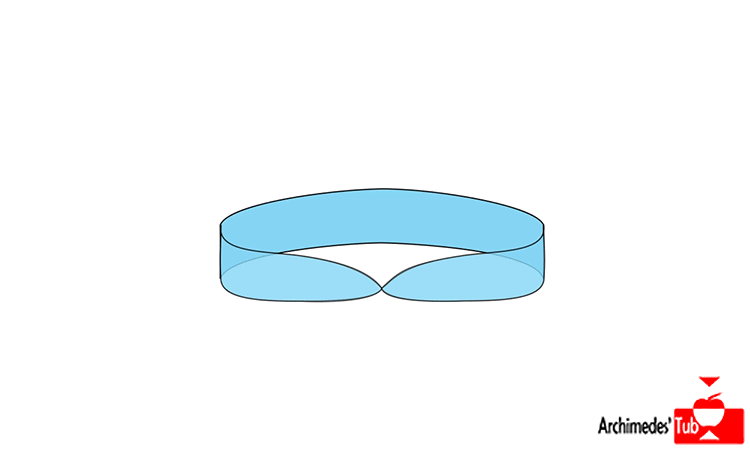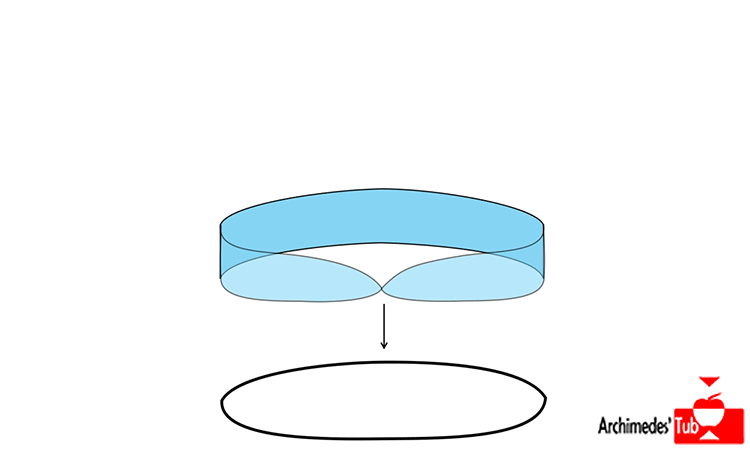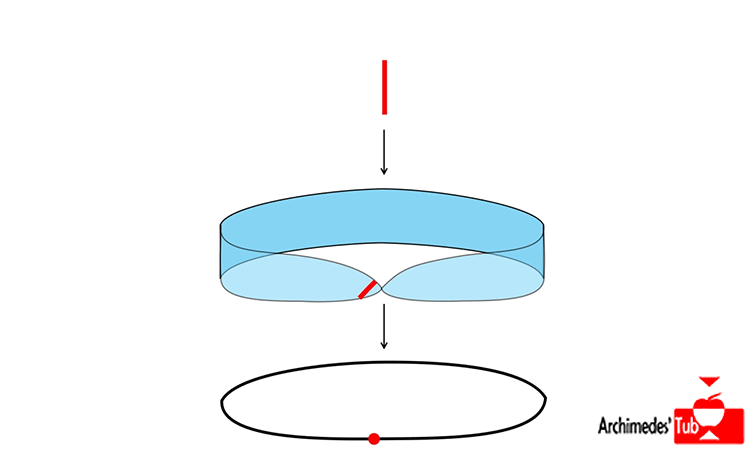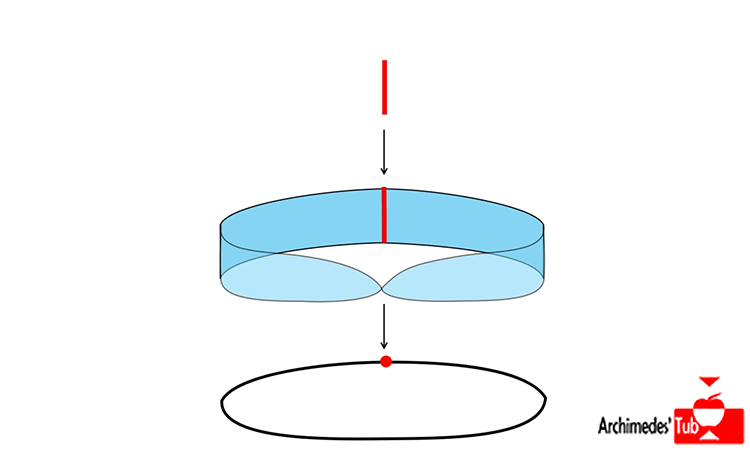
La cinta de Möbius es también el germen y ejemplo ilustrativo de un concepto profundo en topología, el concepto de FIBRADO.
Un fibrado es un espacio que se divide en regiones que son un producto cartesiano, ¡aunque el espacio de forma global puede no serlo!
La cinta Möbius de es localmente un producto de intervalos como puede verse en la animación, pero globalmente NO es el producto de la circunferencia por el intervalo (¡que sería un cilindro, claro esta!).
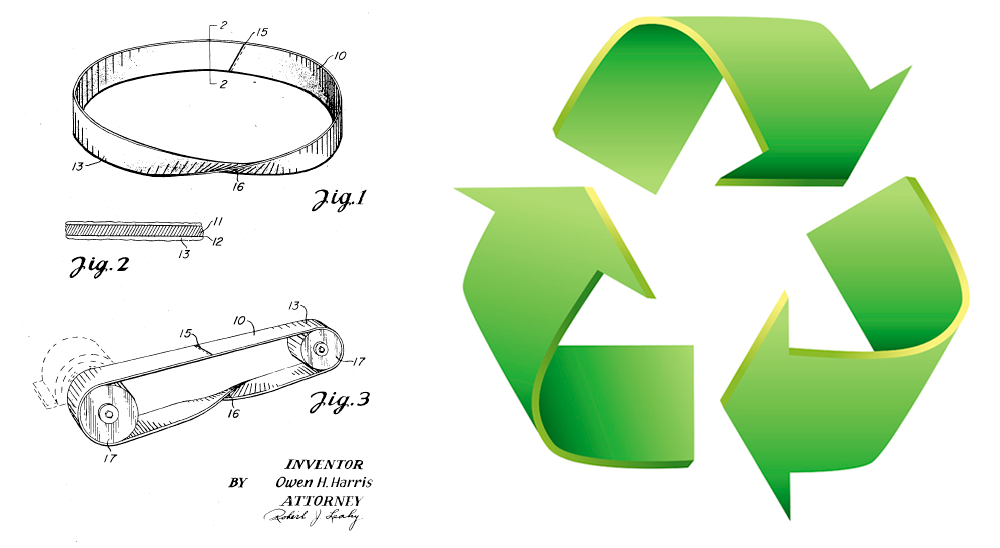
Pero no carguemos demasiado las tintas y volvamos al mundo real. Además de como objeto puramente matemático. La cinta ha sido fuente de multitud de patentes.
Las correas de transmisión de los coches, o las cintas transportadoras de supermercados y aeropuertos van desgastándose debido al rozamiento. Pero tan solo la cara exterior de esta cinta se desgasta. Imaginémonos una cinta de Möbius en lugar de una cinta convencional. Al tener una sola cara “ambas caras” de la cinta sufren el desgaste y ¡su duración sería el doble!
También ha sido utilizado con profusión para logos de todo tipo. Sin ir más lejos, el símbolo universal de reciclaje es una banda de Möbius.
Y sin ir muy lejos, el logo del MATHEMATISCHES FORSCHUNGSZENTRUM OBERWOLFACH, en el que me encuentro ahora mismo apurando mis últimos días ¡también es una banda de Möbius!
Lo más gracioso es que, cómo nos cuenta Martin Gardner en “Mathematics, Magic and Mystery”, la cinta de Möbius se ha utilizado por magos desde hace por lo menos 70 años.
Veamos uno de estos trucos: El Mago invita a dos espectadores para que le ayuden. Saca tres cintas largas de papel y las da a examinar a los espectadores mientras forma con cada una de ellas un círculo, pegando sus extremos.
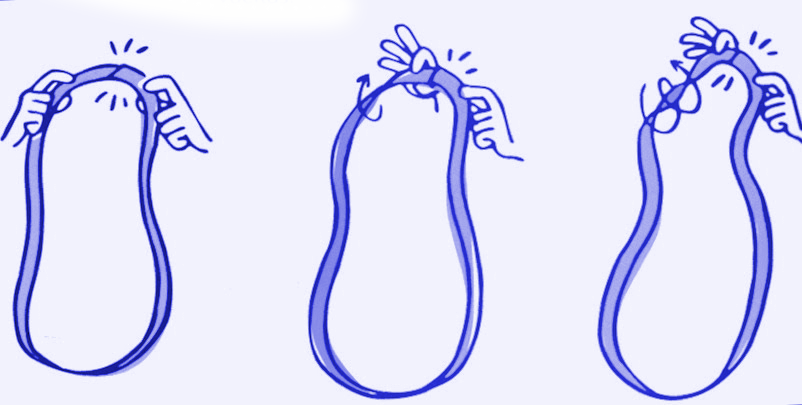
El mago dice que necesita seis círculos en vez de los tres que tiene. Así que agarra unas tijeras y se dispone a recortar longitudinalmente su cinta de papel obteniendo 2 cintas de papel igual de largas e invita a los dos espectadores a hacer lo mismo.
Los Ayudantes se disponen a recortar sus respectivas cintas y para sorpresa de todos, a uno de ellos las dos cintas en vez de separadas le quedan ENLAZADAS entre sí, y al otro en vez de dos, le queda UNA SOLA CINTA el doble de larga ¡MAGIA!
El secreto del truco consiste en que el mago construye su cinta como un cilindro. Mientras que a uno de los ayudantes le da un giro de 180° antes de pegarla obteniendo una cinta de Möbius, y al segundo un giro de 360°.
Os invito a que construyáis estas cintas y comprobéis el efecto. Lo suyo sería tratar de probar matemáticamente porqué se obtiene dicho efecto, porque no olvidemos que todo esto no es magia…ES MATEMÁTICA.