De todas las historias sobre John Nash (que murió hoy hace 3 años y cuya vida ha sido llevada al cine protagonizada por el gladiador Russell Crowe ni más ni menos), hay una pequeña y exquisita que ha llamado poco la atención. A la sazón estudiante de Princeton, Nash inventó un juego para entretenerse sobre las baldosas hexagonales de los baños de la universidad, el juego de Hex. Consiste en un tablero de dimensiones nxn para dos personas en el que cada jugador trata de llegar al lado opuesto dificultando a su vez que el adversario llegue https://es.wikipedia.org/wiki/Hex_(juego)
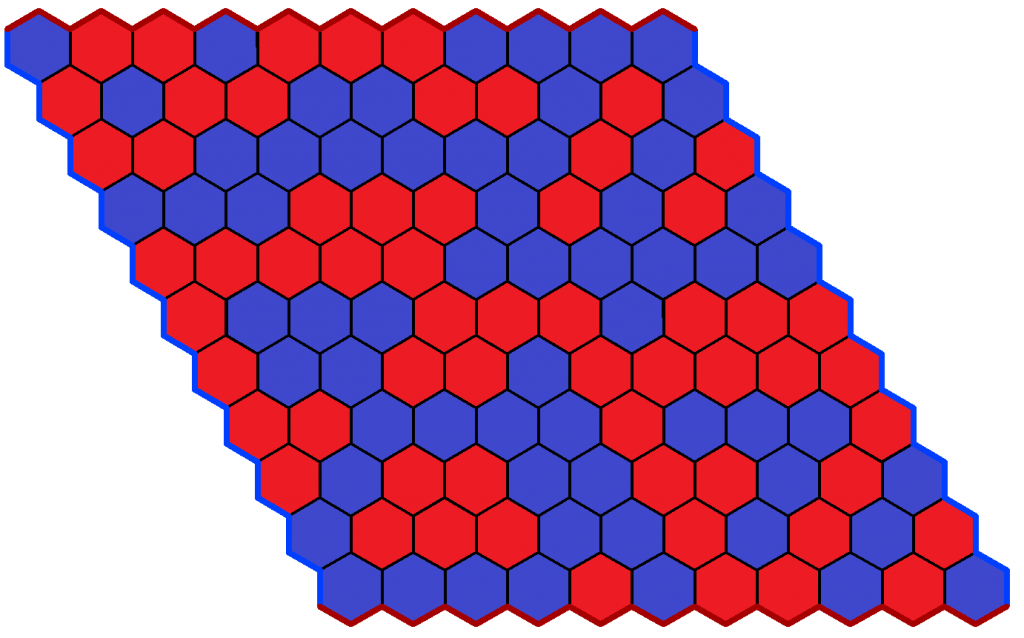
Se puede probar que el juego nunca puede acabar en tablas, algo bastante intuitivo pues si tratamos de construir un puente sobre un río de aguas turbulentas, o el rio arrastra el puente o el puente cruza el río, una de dos. En 1952 Nash probó que el primer jugador tiene de hecho una estrategia óptima.
Pero la historia tiene más miga. Por un lado el juego fue inventado con anterioridad (1942) por el matemático danés Piet Hein (aunque Nash lo descubrió de forma independiente). Y lo más importante, el hecho de que el juego nunca acabe en tablas equivale a un importante teorema topológico “El Teorema del punto fijo de Brouwer”. Curiosamente Nash recibiría en 1994 el premio Nobel de Economía por sus aportes en teoría de juegos y procesos de negociación, en el que los resultados de punto fijo como el de Brouwer tienen un papel destacable. ¿Comenzaría Nash a cimentar su Nobel saltando sobre las baldosas de un baño?
Aquí os dejamos una demostración del Teorema del punto fijo de Brouwer:
[vc_video link=»https://youtu.be/ywhXa_rQJ8Y» el_width=»80″ align=»center»]
